Number System Introduction-Quantitative Aptitude
Dear Aspirants, we are providing here you the each terms that have been used into this number system. All the aspirants should have knowledge about this. It is also come under each competitive exam.
Importance : Being a basic concept of mathematics: 1 and 2 questions on number system are regularly asked in different competitive exams. Its knowledge is also essential to solve other questions.
Scope of questions : Different type of questions like based on fractions, even or odd or whole or divisible or prime or coprime or rational or irrational numbers and related to divisibility, order, ascending, descending, addition, multiplication, inverse numbers may be asked.
Way to success : These questions are solved by different methods. Maximum practice and rechecking is the way to success for this chapter.
Number System : A number system is a system of writing for expressing numbers. It is the mathematical notation for representing numbers of a given set by using digits or other symbols in a consistent manner. It provides a unique representation to every number and represents the arithmetic and algebraic structure of the figures. It also allows us to operate arithmetic operations like addition, subtraction, and division
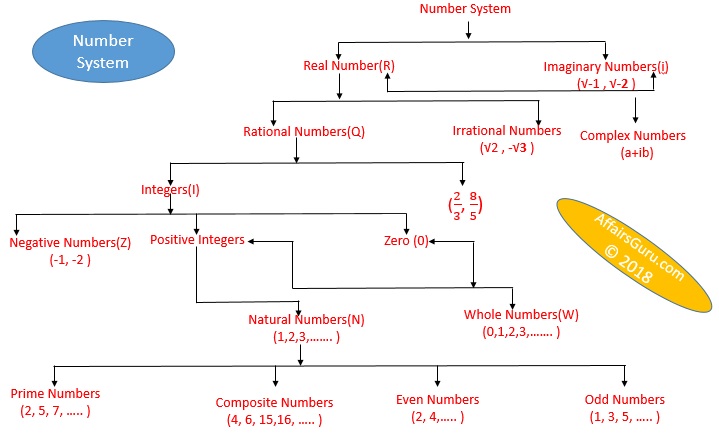
Types of Number System in Maths
Natural Numbers : Set of counting numbers is called natural numbers. It is denoted by N. Where,
$$N=\left\{ 1,2,3,….\infty \right\} $$
Even Numbers : The set of all natural numbers which are divisible by 2 are called even numbers. Its is denoted by E. $$Where,\quad E=\left\{ 2,4,6,8,10,….\infty \right\} $$
Odd Numbers : The set of all natural numbers which are not divisible by 2 are called odd numbers. In other words, the natural numbers which are not even numbers, are called odd numbers. i.e.,
$$O=\left\{ 1,3,5,7,….\infty \right\} $$
Whole Numbers :When zero is included in the set of natural numbers, then it forms set of whole numbers. It is denoted by W. Where,
$$W=\left\{ 0,1,2,3,….\infty \right\} $$
Integers : When in the set of whole numbers, natural numbers with negative sign are included, then it becomes set of integer. It is denoted by I or Z.
$$I=\left\{ -\infty ,..,-3,-2,-1,0,1,2,3,…\infty \right\} $$
Integers can further be classified into negative or positive Integers. Negative Integers are denoted by Z– and positive Integers are denoted by Z+.
$${ Z }^{ – }=\left\{ -\infty ,…-4,-3,-2,-1 \right\} \quad and$$
$${ Z }^{ + }=\left\{ 1,2,3,….\infty \right\} $$
Further 0 is neither negative nor positive integer.
Prime Numbers : The natural numbers which have no factors other than 1 and itself are called prime numbers.
Note that, (i) In other words they can be divided only by themselves or 1 only.As 2,3,5,7,11 etc.
(ii) All prime numbers other than 2 are odd numbers but all odd numbers are not prime number.
Co-Prime Numbers : Two numbers which have no common factor except 1 , are called Co-Prime numbers. Such as ,9 and 16, 4 and 17, 80 and 81 etc.
It is not necessary that two co-prime numbers are prime always. They may or may not be prime numbers.
Divisible Numbers/Composite Numbers : The whole numbers which are divisible by numbers other than itself and 1 are called divisible numbers or we can say the numbers which are not prime numbers are composite or divisible numbers. As, 4,6,9,15,….
Note : 1 is neither Prime Number nor composite number. Composite number may be even or odd.
Rational Numbers : The number which can be expressed in the form of $$\frac { p }{ q } $$ Where p and q are integers and coprime and $$q\neq 0$$ are called rational numbers. It is denoted by Q. These may be positive or negative.
$$e.g.\frac { 4 }{ 5 } ,\frac { 5 }{ 1 } ,-\frac { 1 }{ 2 } \quad are\quad rational\quad numbers.$$
Irrational Numbers : The numbers which are not rational numbers, are called irrational numbers. Such as
$$\sqrt { 2 } =1.414213562……..$$
$$\pi =3.141592653…….$$
Real Numbers : Set of all rational numbers as well as irrational numbers is called Real Numbers. The square of all of them is positive.
Cyclic Numbers : Cyclic numbers are those numbers of n digits which when multiplied by any other number upto n gives same digits in a different order. They are in the same line. As 142857
2 X 142857 = 285714 : 3 X 1428571 = 428571
4 X 142857 = 571428 : 5 X 1428571 = 714285
Perfect Number : If the sum of all divisors of a number N(except N) is equal to the number itself, then the number is called perfect number. Such as, 6, 28, 496, 8128 etc.
The factor of 6 are 1,2 and 3
Since, 6 : 1+2+3=6
28 : 1+2+4+7+14=28
496 : 1+2+4+8+16+31+62+124+248=496
8128 : 1+2+4+8+16+32+64+127+254+508+1016+2032+4064 = 8128 etc.
Note : In a perfect number, the sum of inverse of all of its factors including itself is 2 always.
e.g. Factors of 28 are 1,2,4,7,14 are
$$=\frac { 1 }{ 1 } +\frac { 1 }{ 2 } +\frac { 1 }{ 4 } +\frac { 1 }{ 7 } +\frac { 1 }{ 14 } +\frac { 1 }{ 28 } =\frac { 56 }{ 28 } =2$$
Complex Numbers : Z=a + ib is called complex number, where a and b are real numbers, $$b\neq 0\quad and\quad i=\sqrt { -1 } $$.
$$Such\quad as\sqrt { -2 } ,\sqrt { -3 } \quad etc.$$
So, a + ib or 4 + 5i are complex numbers.
Additive Identity : If a + 0 = a, then 0 {zero} is called additive identity.
Additive Inverse : If a + (-a) = 0, so ‘a’ and ‘-a’ are called additive inverse to each other. As 2 + (-2) = 0
Additive inverse of 2 is -2.
Multiplicative Identity : If a X 1 = a, then 1 is called multiplicative identity. e.g. 3 X 1 = 3 etc.
Multiplicative Inverse : If a X b = 1. then we can say that a and b are multiplicative inverse of each other. As
$$2\times \frac { 1 }{ 2 } =1$$
So, multiplicative inverse of 2 is 1/2.
Thanks you and All the best!
You can join or visit at Facebook Page or Twitter for always keep in touch with further updates.
Read more articles….
| Simplification Formulas | Simplification Rules |
|---|---|
| Square Root and Cube Root | Simplification Questions |
